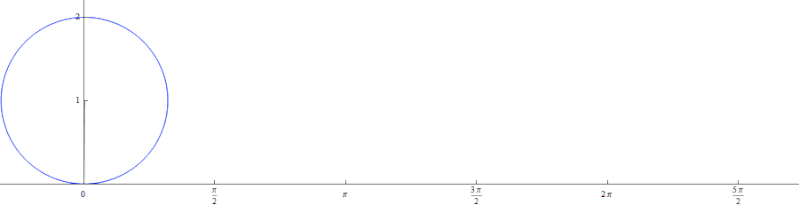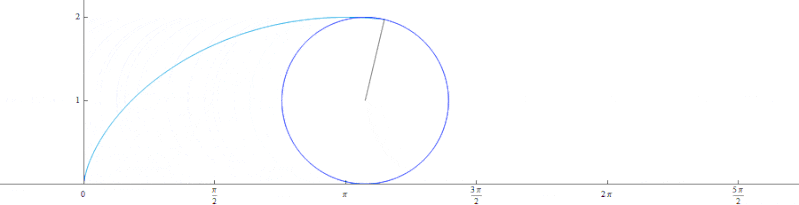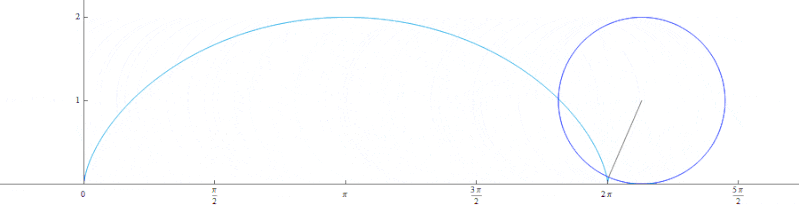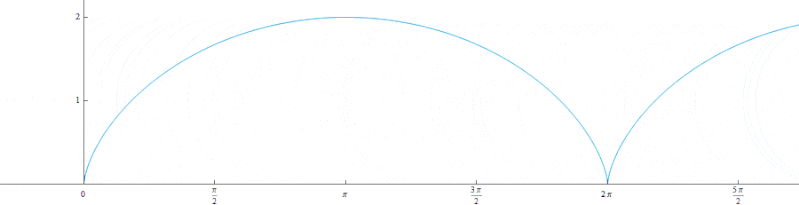サイクロイド理論CYCLOID THEORY

サイクロイド理論とは

サイクロイド理論はサイクロイド曲線に基づいたスイングの理論です。
サイクロイド曲線とは、円を転がしたときに円の外周の一転を繋げていったときにできる曲線です。
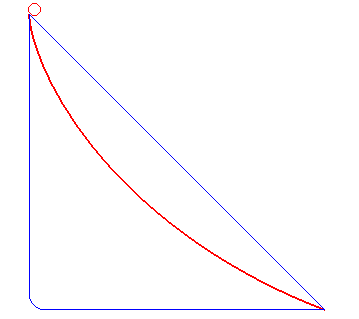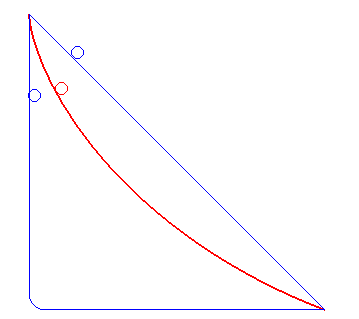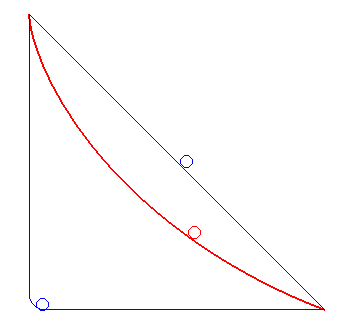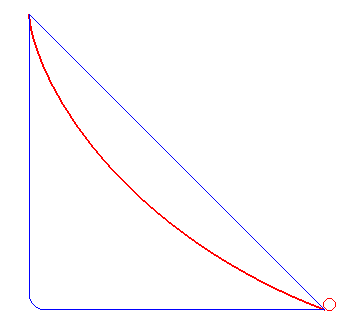
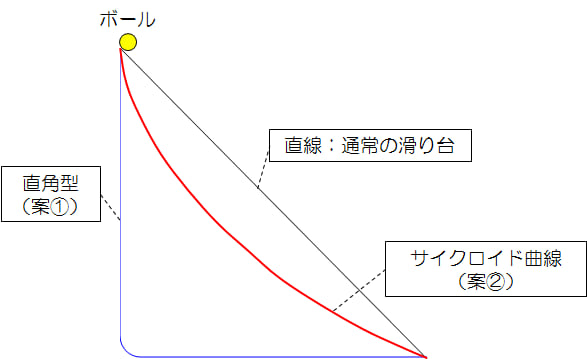
直線とサイクロイド曲線と直角の坂を用意し同じ場所からボールを落とすと
サイクロイド曲線を描いた坂が1番ボールが早く転がるという実験です。
この軌道を描けると効率よく加速をします。

サイクロイドの等時性

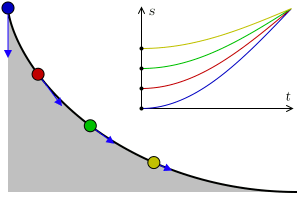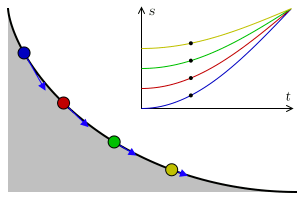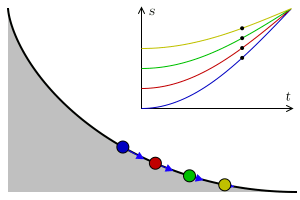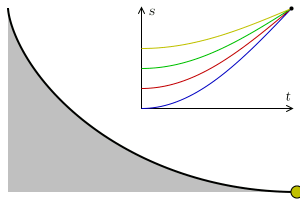
サイクロイドの等時性とは物体が一様重力場の下でその曲線に沿って摩擦なく滑り降りるとき、最下点に達するまでの時間が出発点に依存せず、すべて同じタイミングになります。
なので、サイクロイド曲線上であればどこから振り出しても同じタイミングでバットをボールに当てることができます。